Tutorial: how to make two exactly same balls from one that is also the same as them? The Banach-Tarski paradox.
- Maja Witkowska

- Mar 21, 2025
- 7 min read
Updated: Mar 22, 2025
“ The infinite in mathematics is always unruly unless it is properly treated.”
Edward Kasner, 1878-1955
Most of you might’ve heard of this chocolate riddle:
Firstly we cut a bar of chocolate like in the picture below, then we rearrange them like shown and acquire an additional piece of chocolate that has been created as if from thin air.
Though cool, it’s false as this presentation fills in the missing volume to trick human eyes. Normally the chocolate bar should consist of x smaller volume with x being the volume of the “additional” chocolate piece. The visualisation below shows it perfectly:
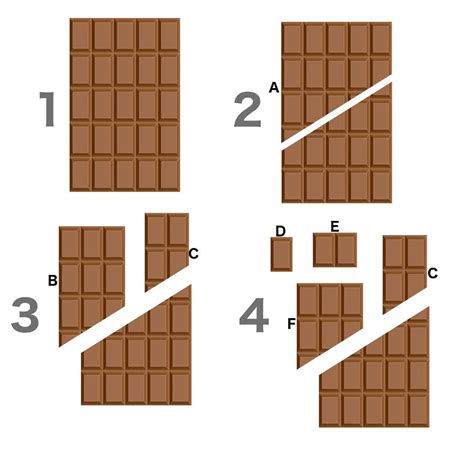
This is almost what the Banach-Tarski paradox represents. How to make two identical objects of the same parameters called X from an object X.

In order to understand this paradox we will have to explore some mathematical concepts.
What’s infinity?
Infinity is certainly not a number on the number liner, rather an interval. The smallest type of infinity is the countable infinity. It consists of natural numbers like 1,2,3,4… and is countable. It means that we are able to say that after 1 is 2, after 4 is 5 and after 5463728 is 5463729, continuing until “infinity”.
Another type of infinity, the one we will need to understand the topic of this article is the uncountable infinity. It is all real numbers that there are and the reason it is uncountable is because we can’t tell what comes after a said element. For example: 0 is first, but what comes next? 0.00000000…1, but no matter how many zeros we write, we can still fit in more zeros and do so infinitely, finally not being able to specify what is the following element. In fact! There are more real numbers between 0 and 1 than there are all natural numbers. To prove this we shall use Geogre Cantor’s diagonal argument:
Firstly, we will assign one real number for every natural number. Then, we pick the nth digit number corresponding to nth natural number e.g.: We take the first digit number from the real number that has 1 assigned to it, second digit number from the second natural number etc. until infinity. We add a 1 to every chosen number and subtract a 1 if it’s a 9. This way we obtain a number that hasn’t appeared anywhere in our table as it will differ from every other number by at least one element. That’s also why the countable infinity is smaller than the uncountable infinity as the latter is like “countable infinity + x”, ∞/2= ∞
Another fact is that there are the same amount of even numbers that there are of whole numbers. If we were to assign one even number to one natural number, until infinity, we would be able to make a 1:1 ratio, showing that two sets are identical
∞+1 =∞
Now, to show how ∞-1 =∞ holds true I will quickly present the idea of Hilbert’s hotel, also known as the infinite hotel. Let’s imagine that we have a hotel with an infinite amount of rooms and guests. If we want to fit in another guest we can simply assign the next room to the prior guest making one additional room for our new visitor. The same holds for when the guest leaves the hotel, we simply move every guest to a room prior to them. As there are infinite rooms and infinite guests, assigning a former or latter room doesn’t change the final result.
Hilbert’s hotel applied to a circle
As we all know, a circumference of a circle is C=2r, which will always be an irrational number as is irrational. That means if we were to pick a point P1 on a circle and every radius length later draw another point (P2), etc. we would never end up on the same point. Now think back to Hilbert's hotel. If I were to remove a bit from our circle and move the point P1 to fill in the bit we took, then the point P2 to fill in the hole after P1 etc. until infinity, I would eventually end up with a whole circle and a bit that I took away as -1 = .
The Hyperwebster, a step away from madness
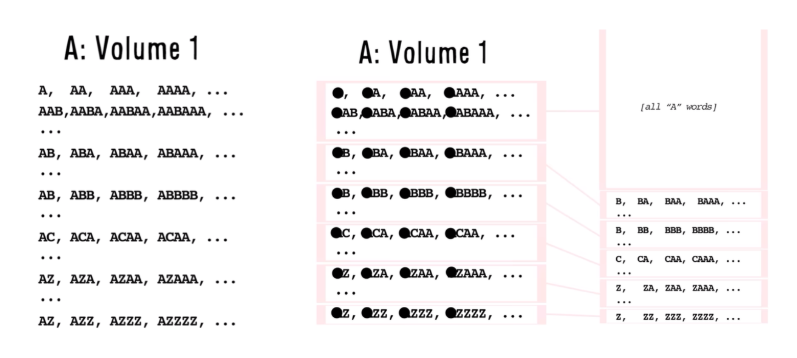
Lastly, I would like to present an idea of Ian Stewart called the Hyperwebster. Essentially it is a dictionary that consists of every word anyone could ever think of made from 26 letters of the English alphabet.
Vsause. Showcase of an Hyperwebster. 1 Aug. 2015. YouTube, https://www.youtube.com/watch?v=s86-Z-CbaHA&t=334s. Accessed 2 Mar. 2025.
It starts with a sequence of A’s and ends with a sequence of Z’s. I want to modify it a bit, taking all the words that begin with an A and putting them in an A Volume, that way I can erase the A’s from those words and suddenly, just from the A volume I have created every other possible word + the A volume with the every other word part left (as initially we only took away all words starting with an A). In conclusion we have managed to create 2 almost identical sets from a set just like them.
The Banach-Tarski paradox
Now, we can finally look at the main topic of this article, the Banach- Tarski paradox. In our words, the idea of a hyperwebster but as a sphere. I will base on drawings a lot as it is a very complicated idea. Firstly, we create a 3d sphere, with 2 axes (Y- up, down and X- right, left). We can move freely within the sphere but only in the Y and X direction so up(U), down (D), right(R), left(L) and we cannot go back so moving right and left isn’t allowed as it simply means we haven’t moved at all. Showing this with symbols would mean that any movement coded as LR, RL, UD, DU is equal to nothing.
Let’s look at 4 examples of movement. We decipher every code from the end so LUR means we move right, up, left. Now let’s color code all sequences ending with an L purple, D blue, R red and U orange. Now if we imagine doing this for every possible sequence we would end up with a countably infinite amount of points named and color coded.
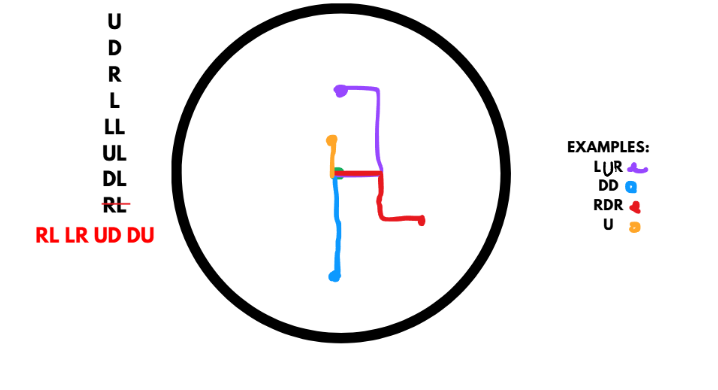
We encounter a problem, as a sphere has an uncountably infinite amount of points we won't be able to color code and name every single of them. The solution to this is to pick a point we have missed and color it green, now instead of the centre being our starting point SP, we will have this new point be our SP. With this issue resolved we continue this process until every single point within the sphere is color coded just once… Except for the poles. For every sequence of R or L rotations the poles are north and south poles. We can get to them with more than one sequence thus color code it more than once and name it more than once. As an example, imagine you follow a code URU, you end up on the north pole but a sequence URUR will be an equally valid name. To avoid this clash we will color code all the poles yellow and since every sequence has two, there will be countably infinitely of them.
Now with every point on the sphere named and color coded we are ready to begin the paradox.
Vsause. The ball color coded into 6 shapes and the centerpoint. 1 Aug. 2015. YouTube, https://www.youtube.com/watch?v=s86-Z-CbaHA&t=334s. Accessed 2 Mar. 2025.
For easier visualisation I’m going to drag a line from the center to every point. Just like that we get 6 shapes of colors and a white center point. Now, let’s try to make two balls from just this one.
Vsause. 1. The ball taken apart into 6 named and color coded shapes 2. chosen sequences with coordinates ending on an L written down. 1 Aug. 2015. YouTube, https://www.youtube.com/watch?v=s86-Z-CbaHA&t=334s. Accessed 2 Mar. 2025.
Let’s take the purple shape, points ending with an L and rotate it. It would mean the same thing as our last move being the R. By writing an R before every L we cancel out RL rotations finishing with rotations beginning with an U or an D. Hence, we have a set consisting of every point ending with an U, D, L and every starting point as the first L cancels out with an R and we’re left with nothing, that’s just like putting a SP. With this one rotation we have created a “ball” consisting of L,U,D,SP. What’s left in order to finish it, we need all the poles, the centerpiece and all the R moves. In order to do that we just add the red shape with R’s, the poles and the center point we extracted from the beginning. This way we have a complete ball with the orange ups, blue downs and green starting points.
To make a second ball, we first take the U shape. We cannot follow the same procedure as before, rotating down and cancelling the U’s and D’s, as it will create the starting points (green) and we will still be left with the green shape from the beginning. In order to avoid that we can just take everything that turns into a starting point and move it from the up piece to the down piece. Of course, all point called e.g. UU after rotating (which will be later on) will create a copy of U in the up and down piece so to avoid that we will put all the U sequences in the down piece. Now if we rotate the piece down, it creates the R piece and the L piece. Adding the down piece with some bits of the up piece we put there earlier, the starting pieces (the green shape) we get R, L, U, D and SP. Now we only need the poles and the centerpoint. Our second ball has small points missing from these poles and the centerpoint. Remember the second point I made about the circle? We draw such circles around every hole in the ball and follow the same procedure as back then making a full circle from a circle with a hole. We do this for every pole hole and the centerpoint hole creating a second full ball. This way we have made two identical copies from the same ball as them.
As impossible as it seems, it's completely true. Basing on axioms and creating such paradoxes I mean but… how? Many scientists believe that small sub- atomic particles can behave this way- doubling its own matter under fast collisions. In the end, 1+1 really may equal 1…
Bibliography:
Vsauce. “The Banach–Tarski Paradox.” YouTube, YouTube, 1 Aug. 2015, www.youtube.com/watch?v=s86-Z-CbaHA&t=334s. Accessed 02.03.2025
Peshin, Akash. “What Is the Infinite Chocolate Paradox?” Science ABC, 17 Feb. 2018, www.scienceabc.com/eyeopeners/infinite-chocolate-paradox.html. Accessed 12 Mar. 2025.



















Comments